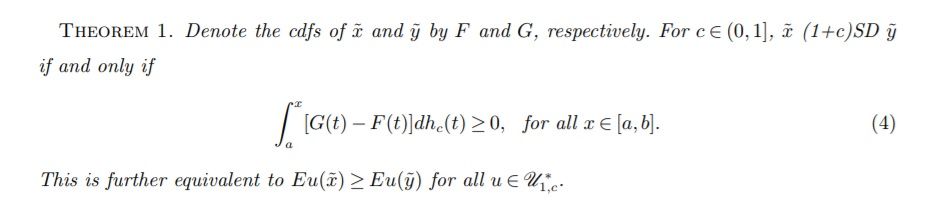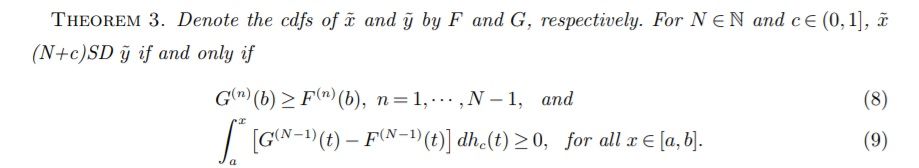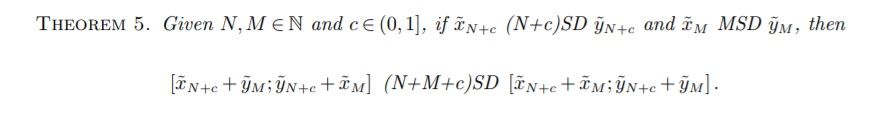| Technical Name | Stochastic Dominance | ||
|---|---|---|---|
| Project Operator | National Taiwan University | ||
| Project Host | 曾郁仁 | ||
| Summary | We develop a continuum of stochastic dominance rules for expected utility maximizers. The new rules encompass the traditional integer-degree stochastic dominance, while between adjacent integer degrees, formulate the consensus of individuals whose absolute risk aversion at the corresponding integer degree has a negative lower bound. |
||
| Scientific Breakthrough | This research has been accepted by Management Science, which is an international top tier academic journal. Management Science serves a role in social science as Nature or Science in science. |
||
| Industrial Applicability | Our findings can be applied to determine comparative statics in decision theory, provide a new approach to derive econometric methodology for empirical research, and establish a new framework for studying individuals' risk preferences in experimental studies. |
||
| Keyword | stochastic dominance risk preferences risk apportionment risk aversion prudence precautionary saving precautionary efforts degree of risk lovingness normal distribution Laplace transfer | ||
- yangsen3183@ntu.edu.tw
other people also saw